Charles Loewner
| Charles Loewner | |
|---|---|
Charles Loewner in '63
|
|
| Born | 29 May 1893 Lány, Bohemia |
| Died | 8 January 1968 (aged 74) Stanford, California |
| Nationality | American |
| Fields | Mathematics |
| Institutions | Stanford University Syracuse University University of Prague |
| Alma mater | University of Prague |
| Doctoral advisor | Georg Alexander Pick |
| Doctoral students | Lipman Bers Adriano Garsia Pao Ming Pu |
Charles Loewner (29 May 1893 Lány, Bohemia – 8 January 1968, Stanford, California) was an American mathematician. His name was Karel Löwner in Czech and Karl Löwner in German.
Loewner received his Ph.D. from the University of Prague in 1917 under supervision of Georg Pick. One of his central mathematical contributions is the proof of the Bieberbach conjecture in the first highly nontrivial case of the third coefficient. The technique he introduced, the Loewner differential equation, has had far-reaching implications in geometric function theory; it was used in the final solution of the Bieberbach conjecture by Louis de Branges in 1985. Loewner worked at the University of Berlin, University of Prague, Louisville University, Brown University, Syracuse University and eventually at Stanford University. His students include Lipman Bers, Roger A. Horn, Adriano Garsia, and P. M. Pu.
Contents |
Loewner's torus inequality
In 1949 Loewner proved his torus inequality, to the effect that every metric on the 2-torus satisfies the optimal inequality
where sys is its systole. The boundary case of equality is attained if and only if the metric is flat and homothetic to the so-called equilateral torus, i.e. torus whose group of deck transformations is precisely the hexagonal lattice spanned by the cube roots of unity in 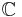 .
.
Book by Loewner
- Loewner, C.: Theory of continuous groups. Notes by H. Flanders and M. Protter. Mathematicians of Our Time 1, The MIT Press, Cambridge, Mass.-London, 1971.
See also
References
- Berger, Marcel: À l'ombre de Loewner. (French) Ann. Sci. École Norm. Sup. (4) 5 (1972), 241--260.
- Loewner, Charles; Nirenberg, Louis: Partial differential equations invariant under conformal or projective transformations. Contributions to analysis (a collection of papers dedicated to Lipman Bers), pp. 245--272. Academic Press, New York, 1974.